My Fascination with 17

There's something about the number 17 that has always captured my imagination. I can't quite put my finger on why, but it has always felt special to me. Perhaps it's the way it keeps appearing in my life at important moments. Firstly, I was born on a 17! Also, My 17th birthday was unforgettable—I spent it on the terrace of the mathematics department at IISc Bangalore during PROMYS India 2023. That day, surrounded by friends and the hum of mathematical conversations, remains one of my most cherished memories. The number 17, in a way, feels like a constant companion.

This quiet fascination started long before my 17th birthday. It was always a number that stood out, popping up in unexpected places and drawing my attention. Maybe it's just coincidence, or maybe there's something inherently intriguing about it. Whatever the reason, I've always felt a particular fondness for 17, and recently, while reading An Encyclopaedia of Curious and Interesting Numbers by David Wells, I was thrilled to discover the various properties of 17.

A Few Properties of 17

The period of 1/17 is of maximal length. 1/17= 0.05882 35294 11764 7 . It is the second prime number with this property, The first being 7 .

One fact about 17 is that it is the third Fermat prime. Fermat primes are a special kind of prime number that can be written in the form

Pierre de Fermat conjectured that all numbers of this form would be prime, but he was later proven wrong by Leonhard Euler, who showed that for n=5 the expression does not produce a prime. The only known Fermat primes are for n=0, 1, 2, 3 and 4 — and 17 fits neatly into this exclusive club.

Historically, 17 also has a unique connection to ancient mathematics. It is the largest number whose square root was proven to be irrational by Theodorus of Cyrene. He could have proved, very easily, that the square root of all primes p is irrational. Yet he chose to demonstrate irrationality only till 17. I believe its probably because for numbers higher than 17 he wouldn't be able to draw such a spiralling wheel without some lines overlapping each other.

Wheel of Theodorus

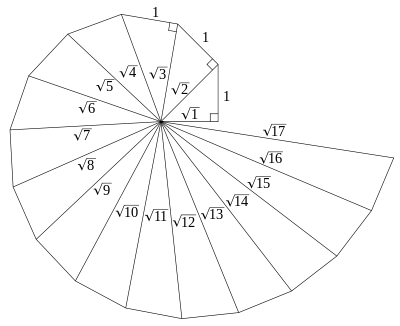
Another fascinating property of 17 involves geometric construction. At the age of just 18, Carl Friedrich Gauss proved that a regular 17-sided polygon (called a heptadecagon) could be constructed using only a ruler and compass.

An Illustration of the Construction

This ground-breaking result revitalized the ancient Greek quest for geometric constructions and demonstrated that certain polygons could indeed be constructed if their corresponding Fermat number was prime. The elegance of Gauss's proof is still celebrated as one of the most beautiful achievements in classical geometry.

There is a very good video on Gauss's Theodorus of Cyrene on Numberphile. I used to (and still do) occasionally try to construct a Heptadecagon by only using a ruler and compass. I have never succeeded, as the errors stack up very quickly.

The Numberphile Video about the Heptadecagon

One of my favourite properties about 17 involves prime-generating polynomials. Ever since I first stumbled upon these polynomials they are a constant source of fascination for me.

The polynomial x^2 +x+17 produces prime numbers for every integer value of  from 0 to 15. This is one of the most well-known examples of a prime-generating formula. In fact, it shares a similar allure with Euler's polynomial x^2 +x+43 , which generates primes for  through 39 and remains the most effective quadratic prime-generator known.

I often wonder why such numbers just pop out seemingly out of nowhere in such problems.

Like for example, let us choose numbers a, b, c, ... in the interval (0, 1) such that a and b are in different halves of the interval. a, b and c are in different thirds of the interval. a, b, c and d are in different quarters of the interval and so on. Not more than 17 numbers can be chosen,

How does 17 pop up in here? Hint: It has something to do with the harmonic series.

In many ways, my fascination with 17 mirrors my broader love for mathematics—the delight of discovering hidden structures, the thrill of solving a puzzle, and the joy of finding connections in unexpected places. Whether it's a Fermat prime, a geometric wonder, or a simple personal milestone, 17 never ceases to amaze me. Perhaps, like a good cricket match (like the India-Australia match which is happening tomorrow), the beauty of mathematics lies in its unpredictability and the endless possibilities it holds.